technical-tips
材料の座屈強度
材料の座屈強度|オイラー座屈・細長比・座屈係数の基礎と設計ポイント
本稿では材料の座屈強度を、新人機械設計者向けに座屈の基本原理・オイラーの座屈式・細長比の考え方から、材料別比較表・計算例・設計時の注意点まで体系的に解説します(単位系はSI、JIS前提)。
座屈の基本原理
細長い圧縮部材は、圧縮応力が高くなると軸方向の圧縮破壊に先立って横方向に不安定変形(座屈)することがあります。座屈は形状・支持条件・材料弾性率に強く依存し、強度(降伏)よりも座屈安定性が支配的になる領域があります。
オイラーの座屈式と境界条件
弾性座屈の臨界荷重 ![]() は以下で与えられます。
は以下で与えられます。
![]()
ここで、![]() :ヤング率、
:ヤング率、![]() :弱軸に対する断面二次モーメント、
:弱軸に対する断面二次モーメント、![]() :部材長、
:部材長、![]() :支持条件による有効長さ係数です。
:支持条件による有効長さ係数です。
- 両端ピン:

- 片持ち(固定–自由):

- 固定–ピン:

- 両端固定:

丸棒の断面特性:
![]()
(![]() :直径、
:直径、![]() :断面積、
:断面積、![]() :回転半径)
:回転半径)
細長比と座屈応力
座屈挙動は細長比 ![]() で整理します。
で整理します。
![]()
![]() はオイラー座屈応力で、
はオイラー座屈応力で、![]() が大きいほど座屈しやすくなります。
が大きいほど座屈しやすくなります。
降伏応力 ![]() との境界(オイラー適用限界)は
との境界(オイラー適用限界)は ![]() より
より
![Rendered by QuickLaTeX.com \[ \lambda_e=\pi\sqrt{\frac{E}{\sigma_y}} \]](https://fa-cty.com/wp/wp-content/ql-cache/quicklatex.com-3996ac8a541db60a2d278beebeedd0bc_l3.png)
で近似できます。一般に ![]() では弾性座屈(オイラー領域)、
では弾性座屈(オイラー領域)、![]() が小さいと降伏(塑性)またはジョンソン近似領域が支配的です。
が小さいと降伏(塑性)またはジョンソン近似領域が支配的です。
材料別の比較(目安値)
| 材料 | ヤング率 E [GPa] | 降伏応力 σy [MPa] | 境界細長比 λe ≈ π√(E/σy) | 備考 |
|---|---|---|---|---|
| 一般構造用鋼(SS400) | 200 | 245 | ≈ 90 | 弾性率が高く座屈に有利 |
| ステンレス鋼(SUS304) | 193 | 205 | ≈ 96 | 耐食性は良いが E は鋼よりやや低い |
| アルミ合金(A6061-T6) | 69 | 276 | ≈ 50 | E が低く細長部材は座屈に不利 |
計算例|片持ち丸棒(ステンレス)φ5・L=100 mm の座屈強度
条件:材料=ステンレス(SUS304相当, ![]() )、断面=丸棒
)、断面=丸棒 ![]() 、長さ
、長さ ![]() 、支持=片持ち(固定–自由,
、支持=片持ち(固定–自由, ![]() )、安全率
)、安全率 ![]() 。
。
- 断面特性:
![Rendered by QuickLaTeX.com \[ I=\frac{\pi d^4}{64}=\frac{\pi(5^4)}{64}\times10^{-12}\approx3.07\times10^{-11}\,\mathrm{m^4} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20343%2039%22%3E%3C/svg%3E)
![Rendered by QuickLaTeX.com \[ A=\frac{\pi d^2}{4}=\frac{\pi(5^2)}{4}\times10^{-6}\approx1.96\times10^{-5}\,\mathrm{m^2} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20333%2039%22%3E%3C/svg%3E)
![Rendered by QuickLaTeX.com \[ r=\frac{d}{4}=1.25\,\mathrm{mm} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20134%2036%22%3E%3C/svg%3E)
- 細長比:
![Rendered by QuickLaTeX.com \[ \lambda=\frac{K L}{r}=\frac{2\times100}{1.25}=160\quad(\text{> } \lambda_e\approx96 \Rightarrow \text{オイラー領域}) \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20333%2037%22%3E%3C/svg%3E)
- オイラー臨界荷重:
![Rendered by QuickLaTeX.com \[ P_\mathrm{cr}=\frac{\pi^2 E I}{(K L)^2} =\frac{\pi^2\times193\times10^9\times3.07\times10^{-11}}{(0.2)^2} \approx1.46\times10^3\,\mathrm{N} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20479%2045%22%3E%3C/svg%3E)
- オイラー座屈応力:
![Rendered by QuickLaTeX.com \[ \sigma_\mathrm{cr}=\frac{P_\mathrm{cr}}{A}\approx\frac{1.46\times10^3}{1.96\times10^{-5}} \approx7.44\times10^{7}\,\mathrm{Pa}=74\,\mathrm{MPa} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20398%2039%22%3E%3C/svg%3E)
- 許容座屈荷重(安全率
 ):
):![Rendered by QuickLaTeX.com \[ P_\mathrm{allow}=\frac{P_\mathrm{cr}}{n}\approx\frac{1461}{2}\approx730\,\mathrm{N} \]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20224%2037%22%3E%3C/svg%3E)
結論:片持ち・細径・短尺でも細長比 ![]() と比較的大きく、許容座屈荷重は約 0.73 kN 程度に制限されます。曲げ荷重が同時に作用する場合はさらに余裕を見る必要があります。
と比較的大きく、許容座屈荷重は約 0.73 kN 程度に制限されます。曲げ荷重が同時に作用する場合はさらに余裕を見る必要があります。
設計時の注意点(チェックリスト)
- 支持条件の厳密化:実機の拘束は理想境界より甘くなることが多く、実質的に K が大きくなる(座屈に不利)。固定長さ・はめあい・治具たわみを考慮。
- 初期たわみ・真直度:初期曲がりや偏心荷重は座屈耐力を低下。加工公差・組立誤差・同軸度を管理。
- 荷重条件:純圧縮だけでなく横方向荷重や曲げモーメント同時作用を評価(座屈は曲げに敏感)。
- 弱軸で評価:開断面・非対称断面は最小 Iで評価。配向により座屈方向が変わる。
- 座屈 vs 降伏の判定:
 が小さい領域では降伏・ジョンソン近似が支配。必要に応じて降伏安全率も併用。
が小さい領域では降伏・ジョンソン近似が支配。必要に応じて降伏安全率も併用。 - 中間支持・ブレース:中間支持の追加で有効長さを短縮し耐力を大幅に改善。
- 弾性率と材料選定:同じ強度でも
 が高い材料ほど座屈に有利(鋼 > ステンレス ≫ アルミ)。
が高い材料ほど座屈に有利(鋼 > ステンレス ≫ アルミ)。 - 環境影響:高温は
 低下、腐食は断面減少。油ミスト・粉塵・腐食環境では保護処置を検討。
低下、腐食は断面減少。油ミスト・粉塵・腐食環境では保護処置を検討。 - 安全率と検証:不確かさが大きい場合は座屈に対し高めの安全率と試作検証を組み合わせる。
早見:境界条件と有効長さ係数 K
| 境界条件 | K | 有効長さ | 特徴 |
|---|---|---|---|
| 両端固定 | 0.5 | 0.5L | 最も座屈に強いが実現が難しい |
| 固定–ピン | ≈0.7 | 0.7L | 片側回転自由 |
| 両端ピン | 1.0 | L | 基準ケース |
| 片持ち(固定–自由) | 2.0 | 2L | 最も座屈に不利 |
実務メモ
- まず
 を計算し、
を計算し、 ならオイラー式で、そうでなければ降伏側チェックも行う。
ならオイラー式で、そうでなければ降伏側チェックも行う。 - 丸棒は
 。細長比を下げる最短手は「直径を上げる」か「中間支持を設ける」こと。
。細長比を下げる最短手は「直径を上げる」か「中間支持を設ける」こと。 - 片持ちは K が大きく不利。可能なら両端拘束や支持点追加を検討。
- 曲げ・衝撃・偏心がある時は、座屈計算に加えて有限要素法(FEM)や試作で余裕を確認。


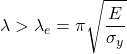 ならオイラー式で、そうでなければ降伏側チェックも行う。
ならオイラー式で、そうでなければ降伏側チェックも行う。